To those who do not know mathematics, it is difficult to get across a real feeling as to the beauty, the deepest beauty, of nature…If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in.
The Character of Physical Law (1965)
Richard Feynman
This term I have been teaching a new first year undergraduate module, Mathematics for Computing, in which I have been trying to impart a little bit of love for mathematics. While we have covered a number of underpinning topics relevant to computer science, such as propositional logic, set theory and number theory, I have also tried to show that there are a multitude of clever little tricks that can make arithmetic and performing seemingly complex calculations that little bit easier. And in doing so, I was reminded of the mathematical prowess of Richard Feynman as well as Hans Bethe, Nobel laureate in physics and Feynman’s mentor during the Manhattan Project. Bethe is one of the few scientists who can make the claim of publishing a major paper in his field every decade of his career, which spanned nearly 70 years; Freeman Dyson called Bethe the “supreme problem solver of the 20th century.”
An example of Bethe’s mastery of mental arithmetic was the squares-near-fifty trick (taken from Genius: The Life and Science of Richard Feynman by James Gleick):
When Bethe and Feynman went up against each other in games of calculating, they competed with special pleasure. Onlookers were often surprised, and not because the upstart Feynman bested his famous elder. On the contrary, more often the slow-speaking Bethe tended to outcompute Feynman. Early in the project they were working together on a formula that required the square of 48. Feymnan reached across his desk for the Marchant mechanical calculator.
Bethe said, “It’s twenty-three hundred.”
Feynman started to punch the keys anyway. “You want to know exactly?” Bethe said. “It’s twenty-three hundred and four. Don’t you know how to take squares of numbers near fifty?” He explained the trick. Fifty squared is 2,500 (no thinking needed). For numbers a few more or less than 50, the approximate square is that many hundreds more or less than 2,500. Because 48 is 2 less than 50, 48 squared is 200 less than 2,500 — thus 2,300. To make a final tiny correction to the precise answer, just take that difference again — 2 — and square it. Thus 2,304.
Bethe’s trick is based on the following identity:
For a more intuitive geometric proof of this formula, imagine a square patch of land that measures on each side:
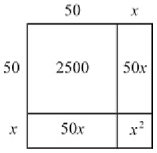
Its area is , which is the value we are looking for. As you can see in the diagram above, this area consists of a 50 by 50 square (which contributes the
to the formula), two rectangles of dimensions 50 by x (each contributing an area of
, for a combined total of
), and finally the small x by x square, which gives an area of
, the final term in Bethe’s formula.
While Feynman had internalised an apparatus for handling far more difficult calculations (for which he became famous for at Los Alamos, such as summing the terms of infinite series or inventing a new and general method for solving third-order differential equations), Bethe impressed him with a mastery of mental arithmetic that showed he had built up a huge repertoire of these easy tricks, enough to cover the whole landscape of small numbers. Bethe knew instinctively that the difference between two successive squares is always an odd number (the sum of the numbers being squared); that fact, and the fact that 50 is half of 100, gave rise to the squares-near-fifty trick.
Unfortunately, the skill of mental arithmetic that did so much to establish Bethe’s (as well as Feynman’s) legend was doomed to a quick obsolescence in the age of machine computation; a “feel for numbers” (or perhaps “quantities”) appears to be a dying art today.
I wonder at what point the ‘squares near fifty’ fails to work. So I tried a range of numbers for x from 12 right through to 114. The mental maths does get more tricky the further away from 50 you get and I made more mistakes. I then worked out that for square numbers close to 100 it was easier to work on (100 + x) squared = 10000 + (x * 200) + x squared. Try it. I imagine this rule can be modified for other commonly known squares, eg squares near 500 etc.
Thanks for a great piece of Maths to start the day.
My personal favourite trick is calculating sums of series: imagine two teams of n people shaking hands: each person in each team shakes hands with everyone in the opposite team (but they don’t shake hands at all with anyone from their own team).
How may handshakes are there?
Fairly intuitively, there are : each one of n people shakes hands n times: that is, with everyone in the opposing team.
: each one of n people shakes hands n times: that is, with everyone in the opposing team.
But to see a different way of calculating it, imagine how do they actually do it: one team (the home team, perhaps) lines up, and then the away team comes in: the first away player shakes hands (one handshake); then he moves along, and shakes hands with the next home player, and while he does this, then second away player shakes hands with the first home player (so now we have two additional handshakes), and so on.
This continues until we have n handshakes at once, when the teams are totally lined up.
But then it carries on: the first away player is now finished: he’s shaken hands with everyone. So now we have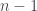 handshakes, then
handshakes, then 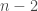 , etc, down to 1.
, etc, down to 1.
So this gives us a nice summation answer:
But we already know that the number of handshakes is .
.
A little bit of manipulation gives us this:
Okay, maybe it’s a not a trick, but it’s pretty neat!
Speaking of summing of series, there is the (probably apocryphal) story of Carl Friedrich Gauss as a 10-year-old schoolboy, who was asked to find the sum of the first 100 integers. The schoolmaster, who had set the task as a punishment, was astonished when Gauss presented the correct answer, 5050, almost immediately.
Gauss had included 0 in the series and rearranged the terms into 50 pairs, each of which totals 100. The 50 pairs together make 5000, which, when added to the unpaired central number, 50, gives the correct answer of 5050.
Further interesting summing facts:
* The sum of the numbers 1 through 10 is 55.
* The sum of the numbers 1 through 100 is 5,050.
* The sum of the numbers 1 through 1,000 is 500,500.
That’s a trick I learned from reading about Gauss; and it’s also a nice little algorithm to use when teaching intro algorithms, e.g., for positive integers why do
int sum(int n) { int tot = 0; while(n) tot += n--; return tot; }when you could just do
int sum(int n) { return n + n * (n - 1) / 2; }Oh, just noticed that Tom’s also mentioned this.
I find generally that or
or  are generally useful in computing squares as you tend to pick x and y that you know the square of: usually possible if you pick an x that is in some sense “round” (like 50 or 100) and a y that is in some sense “small” (say between 2 and 30). I guess these values in some sense hashed or cached (I’m not that sure-footed with the computing terminology!) in your head; I suppose this is the scientific value of the anecdote: work with what you do know to find something that you don’t!
are generally useful in computing squares as you tend to pick x and y that you know the square of: usually possible if you pick an x that is in some sense “round” (like 50 or 100) and a y that is in some sense “small” (say between 2 and 30). I guess these values in some sense hashed or cached (I’m not that sure-footed with the computing terminology!) in your head; I suppose this is the scientific value of the anecdote: work with what you do know to find something that you don’t!
I suspect “cached” is the more accurate term here.
Along those lines, I wonder how do we work out, in our heads, on the fly, which previously-solved question is most similar to the problem at hand?
For example, if I want to work out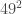 , it’s less than
, it’s less than  , and I already know what
, and I already know what  is.
is.
But what if I want to work out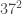 ? Is it
? Is it  , which is
, which is 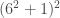 ? Or is it
? Or is it  ?
?
I think that’s the key part — both Feynman and Bethe has a broad arsenal of shortcuts and approximations that they could manipulate to perform rapid mental arithmetic, for example rapidly summing infinite series.
So cached is right — it’s about having a number of different base points from which to start the calculation.
Some handy divisibility rules (HT Futility Closet):
* A number is divisible by 3 if the sum of its digits is divisible by 3.
* A number is divisible by 4 if the number formed by the last two digits is divisible by 4.
* A number is divisible by 8 if the number formed by the last three digits is divisible by 8.
* A number is divisible by 9 if the sum of its digits is divisible by 9.
It’s late, so I can’t verify this, but I guess a number in base 10 is divisible by iff its last n digits are divisible by n.
iff its last n digits are divisible by n.
I imagine the same is true of numbers expressed in base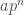 , where p does not divide a.
, where p does not divide a.
When i was in high school, i had a Japanese abacus (soroban) and two books. After about three months, i got to the chapter where it suggests visualizing the device and using it for mental arithmetic. I quickly went through all the examples, including dividing a six digit number by a four digit number. No mistakes. I wanted to know what the limits were. I had a calculator that could show eleven digit answers, and could compute trig functions. I picked an angle, something like 23.7 degrees, converted to radians, and performed the Taylor series expansion for sin(x). In about 35 minutes, i wrote down the answer, which turned out to be correct. At the time, i couldn’t remember numbers easily. It took over a month to memorize ten digits of pi. But this calculation required remembering some 80 digits of intermediate results, such as the previous factorial or x^n. 17! = 355687428096000. So i concluded that anyone could learn this technique and perform miracles. I’m still convinced that it could help everyone. I believe that fear of math is reinforced by every error. This technique reduces errors. As a benchmark, i’ve reduced arithmetic to equivalent digit adds. 48 * 48 has four multiplies, all of which are two digits, so there are 8 digit adds. My trig calculation sustained six digit adds per second. So 48 * 48 = 2304 takes 1.3 seconds, and you don’t have to learn any tricks.
I know a technique that’s more general (you can easily multiply any 2 digit numbers that are close enough) but isn’t quite as fast. You simply choose a “base” number that is close to the 2 numbers you want to multiply, and then add the difference between the “base” and one of the numbers to the other number. Let’s call this new number the “adjusted” number. Then, multiply the adjusted number by the base, and then add the product of the differences of the 2 numbers from the base. I know that probably sounds really confusing, so here are some examples:
(1)
48 * 48
Let’s choose a “base” of 50 because it’s a nice round number. Then, the difference of both 48s from 50 is -2. So the adjusted number is 46. Now, 46 * 50 = 2300 (this is pretty easy to do in your head). Then, add the product of the differences from the base: (-2) * (-2) = 4.
Final answer: 2300 + 4 = 2304.
(2)
26 * 33
Base = 30. Differences are 30 – 26 = -4 and 30 – 33 = 3. So, adjusted number is 29. Notice that it doesn’t matter which number you choose to add the other number’s difference to (26 + 3 = 29 and 33 – 4 = 29); this result is always true. Now, multiply the adjusted number by the base to obtain 29 * 30 = 870 (again, pretty easy to do in your head) and add the product of the differences -4 * 3 = -12.
Final answer = 870 – 12 = 858.
It seems like a lot to remember/calculate, but once you practice it just a little bit you can do it in a few seconds. If you’re wondering why I know this, I was trying to learn a somewhat general arithmetic trick to use in job interviews. Believe it or not, I had to take mental arithmetic tests!